Context-free grammar

Context-free grammars (CFGs) are used to represent large / infinite schemas.

Examples

We'll use an example to directly show how they work. Say we build a calculator to solve word problems: "I have 3 apples. I buy 2 bags of apples. Each bag has 5 apples. How many do I have?"

LLMs hallucinate a lot in math tasks. Instead of using an LLM to do math and get the answer, we decide to use constrained decoding to get the corresponding math expression:

(3 + (5 * 2))

Once we get this expression, we can deterministically calculate it in code to get the answer.

So we need a schema for math expressions with brackets: (7 - 5) + 3, (7 - (5 * 5)) + 3, (7 - (5 * (5 + 11))) + 3, and so on. This is an infinite schema, as math expressions can have infinite nesting depth. In regex, we'll need to chain regex patterns for each nesting depth:

  (
    # Depth 1
    \(\d+ [\+\-\*\/] \d+\)
  )
|
  (
    # Depth 2
    \( ( \(\d+ [\+\-\*\/] \d+\) | \d+ ) [\+\-\*\/] ( \(\d+ [\+\-\*\/] \d+\) | \d+ ) \)
  )
|
  (
    # Depth 3
    \( ( \( ( \(\d+ [\+\-\*\/] \d+\) | \d+ ) [\+\-\*\/] ( \(\d+ [\+\-\*\/] \d+\) | \d+ ) \) | \d+ ) [\+\-\*\/] ( \( ( \(\d+ [\+\-\*\/] \d+\) | \d+ ) [\+\-\*\/] ( \(\d+ [\+\-\*\/] \d+\) | \d+ ) \) | \d+ ) \)
  )
.
.
.

We'll need to chain infinite regex patterns.

Instead, here's a simple CFG that does this:

root ::= expr

expr ::= number | "(" expr op expr ")"
op   ::= "+" | "-" | "*" | "/"
number ::= [0-9]+

It has four parts:

1. Terminals: Elements that cannot expand into other elements. number and op here.
2. Non-terminals: Elements that can expand into other elements. expr here expands into <number> or (<expr> <op> <expr>).
3. Rules: Instructions on how elements can be resolved into actual characters or expanded. Here, root ::= expr, expr ::= number | "(" expr op expr ")", op ::= "+" | "-" | "*" | "/", number ::= [0-9]+ are the rules.
4. Root: How to start production. root ::= expr means every production starts with expr.

To generate output, a CFG starts with the root, which can contain terminals and/or non-terminals. The terminals are resolved into actual characters. The non-terminals expand into other elements (terminals and/or non-terminals), according to the rules. This happens recursively until all the non-terminal elements are expanded into terminals, and then, resolved into actual characters.

We'll show how (7 - (5 * (5 + 11))) + 3 is generated using this CFG:

Step 1

<expr>

Start with the root expression.

Rule: root ::= expr

CFGs don't need to explicitly represent every nesting depth. Instead, they have rules that expand expressions into other expressions, in order to increase nesting depth as and when needed.

Here's a CFG for our Wikipedia schema:

root        ::= "{" "\"title\":" string ",\"link\":" link_value "}"

link_value  ::= root | "null"
string      ::= "\"" ([^"\\] | "\\" .)* "\""

Grammars use PDAs

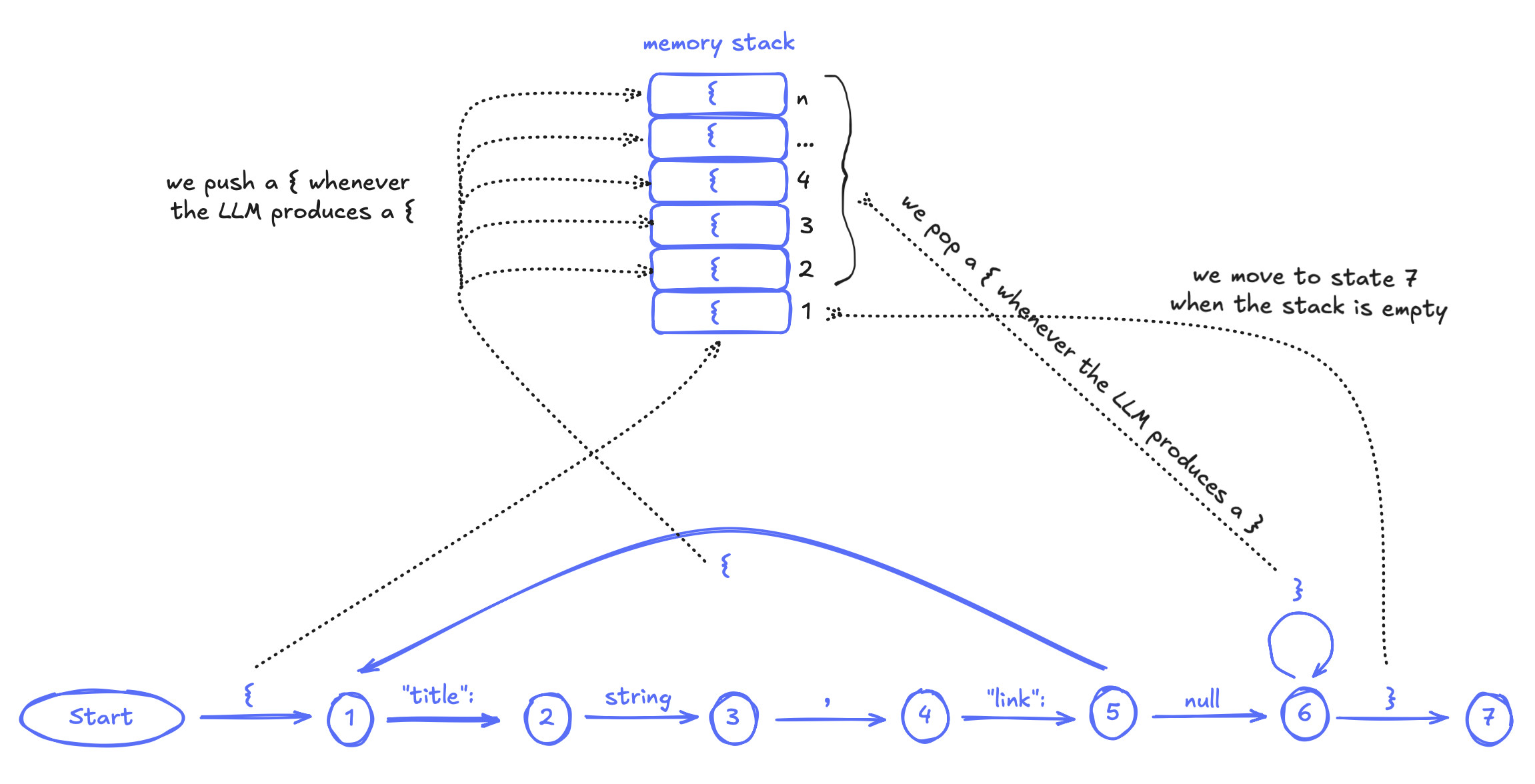
For our purposes, we can see a Pushdown Automaton (PDA) as FSM + stack.

FSMs don't have memory. They can't remember how many times they've seen a nesting character like ( or {, and thus, they can't track nesting depth. A PDA fixes this by adding the stack, which acts as a memory that tracks nesting characters and depth.

Say you want to check if parentheses are balanced in this text: (())

1. Read (: The PDA pushes a marker onto the stack.

2. Read (: The PDA pushes another marker.

3. Read ): The PDA pops one marker off. It "matched" a pair.

4. Read ): The PDA pops the last marker. It "matched" the second pair.

If the stack is empty when the text ends, it means the parenthesis are balanced, and the text is valid. If you have a ) left in the text but the stack is empty, or if the text ends and the stack still has a (, the text is not valid.

A constrained decoding backend converts CFGs into Pushdown Automata (PDAs), and uses the "memory" stack to track nesting depth, as shown above. Here's the PDA for our Wikipedia CFG:

This is a simplified diagram to aid understanding.

Step-by-step walkthrough of our calculator generating (3 + (5 * 2)) for the math problem:

Step 0

What Happens

Start at the root and initialize stack.

Current State

root

expr

Stack State

(Empty Stack)

Current Output