A Comprehensive Guide to Fuzzy Name Matching/Fuzzy Logic
In this blog, we will look at Fuzzy match, the go-to approach in matching things from strings to even DNA sequences.
What is Fuzzy Search?
Fuzzy Search (also called Approximate String Matching) is a technique for identifying two elements of text, strings, or entries that are similar but not the same.
For example, let’s take the case of hotel listing in New York, as Expedia and Priceline show in the graphic below.
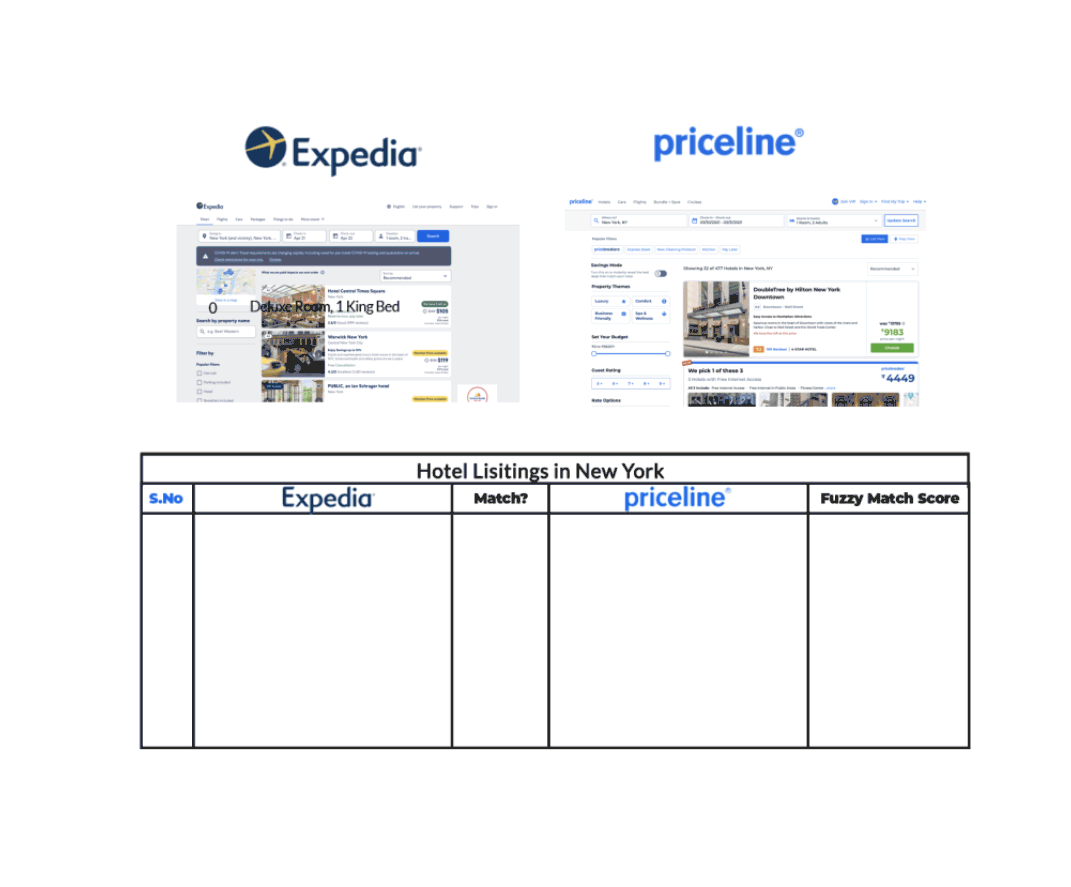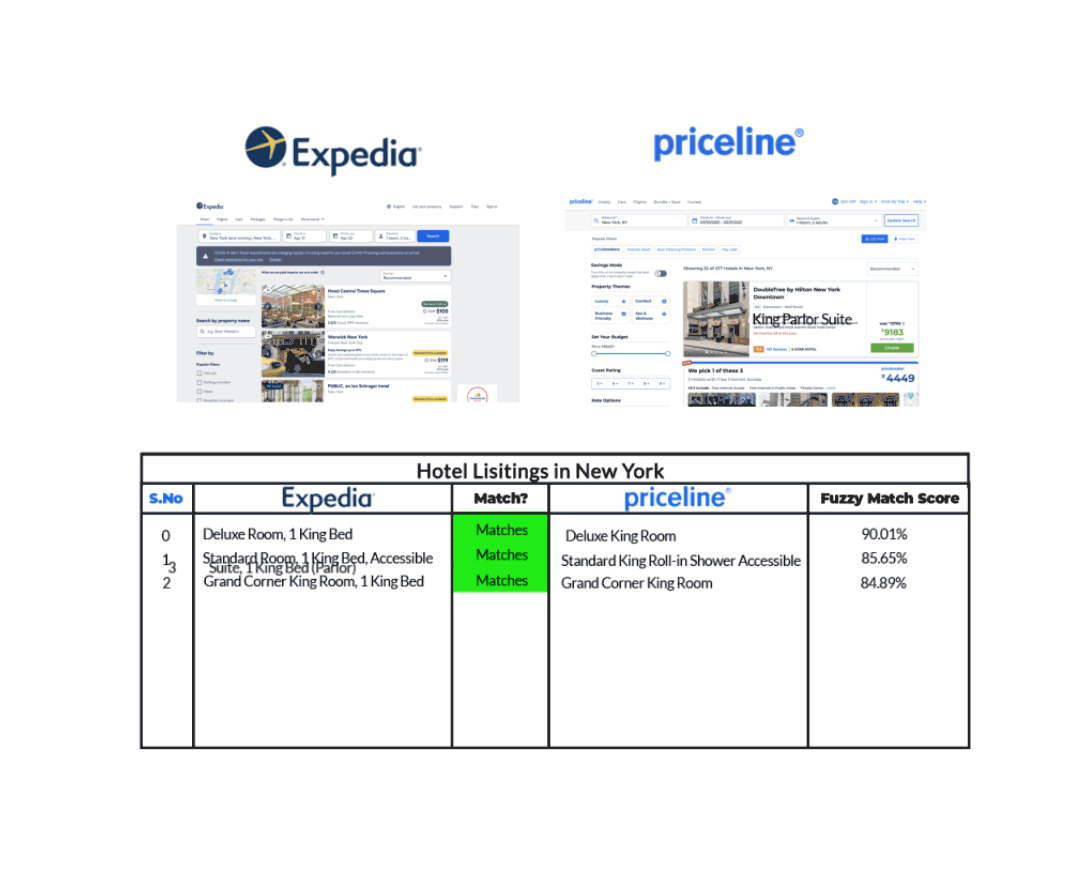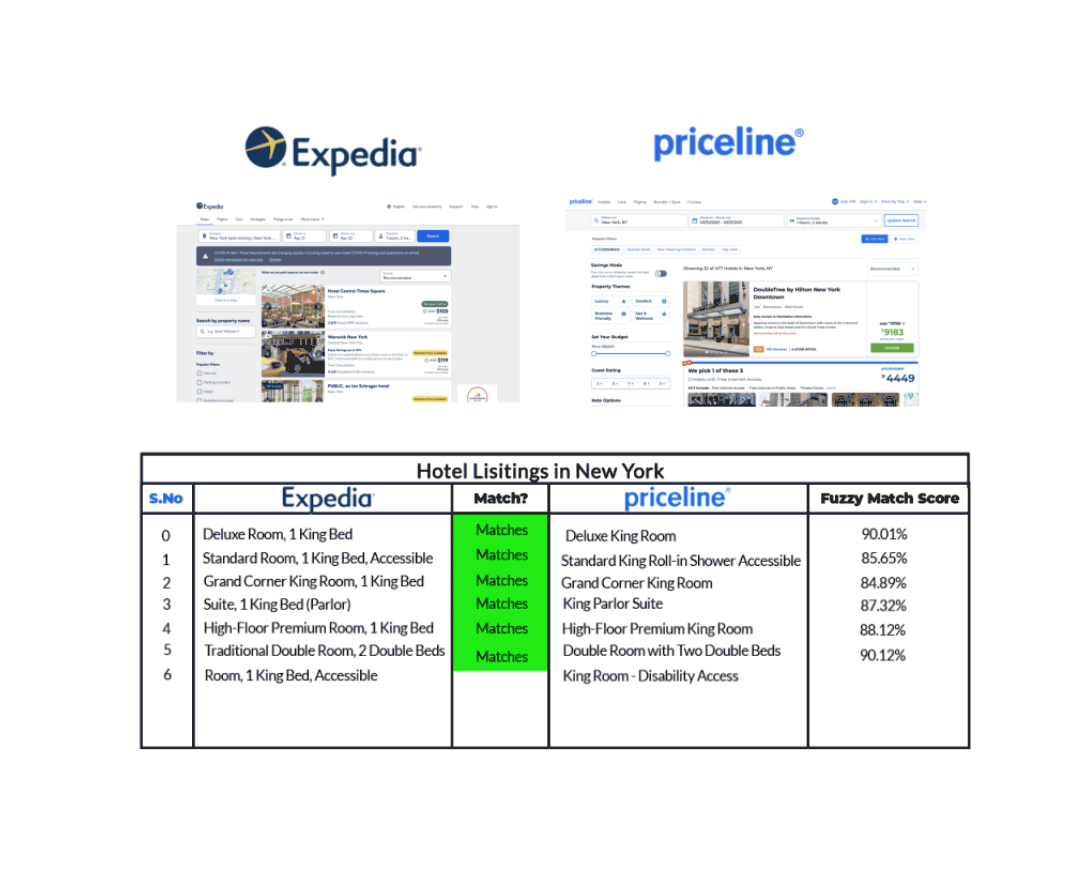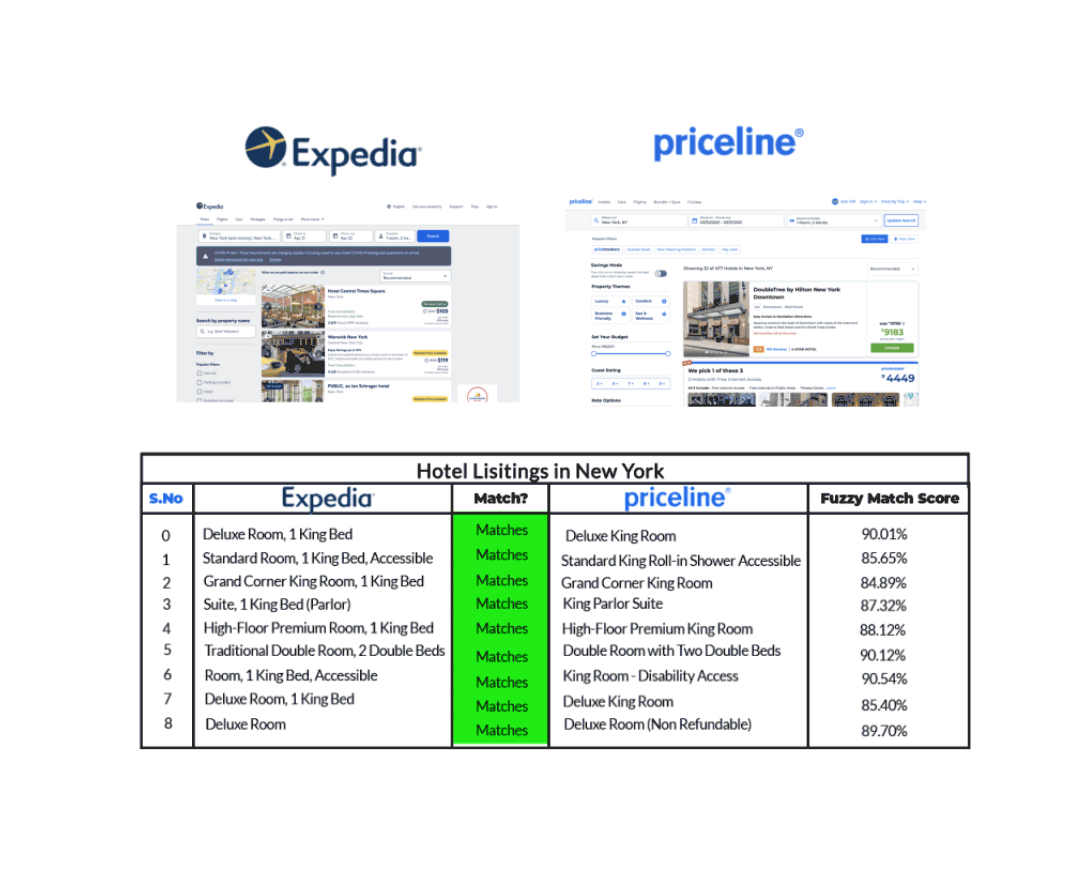
Expedia and Priceline describe the duplicate listing in slightly different ways. Using Fuzzy Matching, which identifies two pieces of text that are approximately similar, we can match the duplicate hotel listing from each site, though their descriptions aren’t the same.
Looking to extract information using Fuzzy Matching? Head over to Nanonets to use the solution that offers advanced Fuzzy Matching!
What is Fuzzy Matching?
Fuzzy Match compares two sets of data to determine how similar they are. It allows for partial matching of sets instead of exact matching. Fuzzy matching is the broad definition encompassing Fuzzy search and identical use cases. Both work similarly and deploy similar algorithms to achieve the matching.
Let’s try to understand the fundamentals of fuzzy logic and matching.
How does Fuzzy Matching or Fuzzy Logic work?
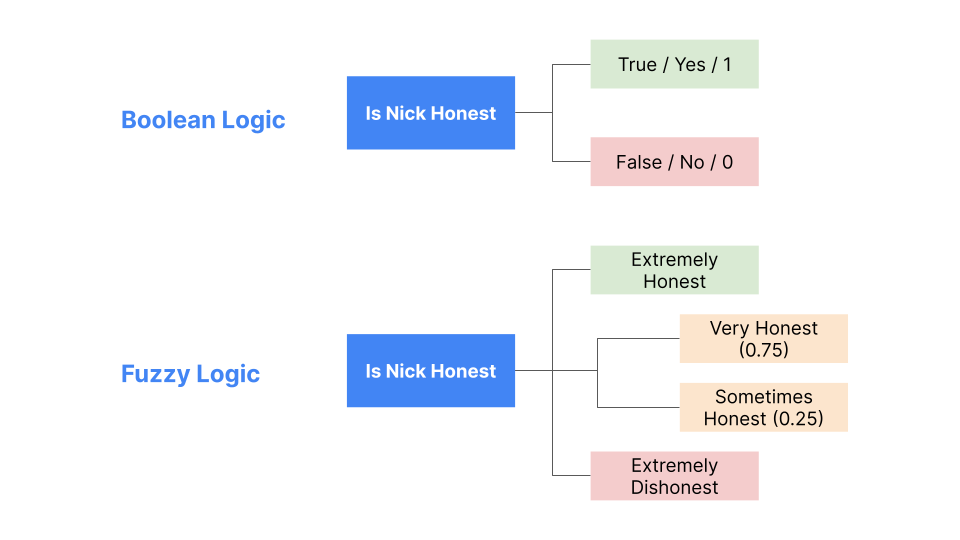
Traditional logic is binary, i.e., a statement is true or false. In the previous example, a record in Table 1 either exactly matched a record in Table 2 or didn’t.
On the contrary, fuzzy logic indicates the degree to which a statement is true. For example, fuzzy rules can indicate that the listings under Expedia potentially correspond to the duplicate listing under Priceline.
Looking to extract information using Fuzzy Matching? Head over to Nanonets to use the solution that offers advanced Fuzzy Matching!
How does Fuzzy Matching help in real-world scenarios?
There are many situations where Fuzzy Matching techniques can come in handy. Let’s look at some real-world examples of using Fuzzy Matching.
1) Creating a Single Customer View (SCV): A single customer view (SCV) refers to gathering all the data about customers and merging it into a single record.
For example, Assume that you manage a restaurant. You might have the following data sources/tables. Table 1 contains information regarding your customers’ order history, and Table 2 contains information about their surfing patterns on the restaurant’s website.
A large organization is bound to have many such tables that it could join to obtain a single customer view. This often requires fuzzy string matching (in our scenario, Tables 1 and 2 must be joined using the Customer Name attribute).
The restaurant could leverage the SCV information as follows: When a regular patron calls to place an order, the restaurant could suggest a new dish based on their order history and the recipes they have surfed. The restaurant could also send customers customized content (new exciting recipes) using the SCV information.
2) Data Accuracy for AI Training:
According to a recent study, over 60% of companies have implemented solutions based on Machine Learning. Data accuracy becomes crucial as companies rely on artificial intelligence and machine learning.
Groundbreaking research is often carried out to improve the accuracy of neural networks and Machine learning technologies. However, more must be done to ensure that these models are fed good-quality data. A great machine learning algorithm without accurate data is analogous to launching a rocket using compressed natural gas to Mars.
Fuzzy string matching can help improve data quality and accuracy by deduplicating and identifying false positives.
3) Fraud Detection:
A good fuzzy string-matching algorithm can help in detecting fraud within an organization. Later in this post, we’ll see how the FAA used fuzzy string matching to single out several pilots for exhibiting fraudulent behavior.
4) Spelling Corrector (Source: http://norvig.com/spell-correct.html)
Nowadays, most of us don’t even bother to find the correct spelling while writing an email; such is the trust we place in modern spelling correctors.
In the following paragraphs, I will describe the basic plumbing of a simple spelling checker.
The following equation is used to find the most probable correction:
Here, P(c) indicates how often the word ‘c’ is used in English. It can be computed by counting the number of times a word appears in a large text corpus. P(w|c) is the probability that the author typed in the wrong word ‘w’ instead of the correct word ‘c.’ P(w|c) depends on our error model.
The following steps are used to find out a corrected spelling:
i) The fuzzy step: Find all the possible valid words having edit distances(Minimum number of single-character substitutions, insertions, or deletions required to transform one string into the other) of 1 and 2 concerning the given word.
(ii) The error model: Assume that the words at an edit distance of 1 are more probable than words at an edit distance of 2(Normally, something more sophisticated should be used for the error model).
We can find the most probable correction since we have P(c) and P(w|c). The algorithm combines fuzzy string matching with probability theory to construct a simple but efficient spelling corrector.
5. Classification of Genome Data ( Source: http://www.ipcsit.com/vol30/019-ICNCS2012-G1021.pdf)
In this work, the authors investigate the problem of determining the group of an unseen genome sequence. They solve the problem of group identification by using a large database of genome sequences.
They try to match the query(unknown) sequence with potential candidates in the database.
Exact matching could be more helpful since the query sequence rarely exactly matches the genome sequences in the database. The authors tackle this problem by using fuzzy matching between the query sequence and the genome database.
The matches are then fed as inputs to a classifier(SVM, backpropagation, etc.) that determines the genome's group.
Hopefully, you are convinced that fuzzy name matching is an important topic and is worth your time.
Looking to extract information using Fuzzy Matching? Head over to Nanonets to use the solution that offers advanced Fuzzy Matching!
Understanding Fuzzy Matching with a Real World Example
Let’s try to understand the concept of fuzzy Matching by considering a real-world example.
If you were given the task of joining multiple tables within this schema to create a single view for customer or product data, how would you proceed?
In theory, if all the data was perfectly clean(no duplicates, no misspelled words etc) we could perform the join operation using appropriate primary and secondary keys. However, real-world data is often very flawed, messy, and inaccurate.
A survey conducted by Gartner points out that “Poor data quality is a primary reason for 40% of all business initiatives failing to achieve their targeted benefits”(https://www.data.com/export/sites/data/common/assets/pdf/DS_Gartner.pdf).
Given that real-world data is bound to be messy, how would we proceed to join individual tables? Consider the example shown in Fig 5.
Let’s say that we want to join the ‘Customers’ and ‘Orders’ tables based on the customer_name attribute. We could use a deterministic rule which is based on strict correspondences between records in table1 and table2.
For instance, a customer name “John Chambers” in table1 is matched with all occurrences of the same customer name(“John Chambers”) in table2.
Although this approach is theoretically sound, it rarely works in practice. For example, if the name “John Chambers” is misspelled as “Jon Chamber” in table2, the resulting join would be inconsistent. How would we solve such a problem?
Fuzzy matching can be useful in such scenarios.
How does Fuzzy Name / Fuzzy String Matching Work?
One of the most critical use cases of fuzzy matching arises when we want to join tables using the name field.
To understand the problem of fuzzy name matching, let us consider the following problem.
Let’s say a marketing company sends out a questionnaire to many people. Some people take the time to fill out the questionnaire, while the rest don’t bother. Now, the same company sends out a different questionnaire after 6 months to the same set of people.
The company stores the responses to the first and second questionnaires in two separate tables. The company would want to join tables 1 and 2 using the ‘name’ attribute as a primary key to merge the collected information.
However, there is no guarantee that a person will fill out the same name in the first and second questionnaires. For example, a person whose official name is “Dr. Jack Murphy” might fill in “Jack” in the first questionnaire and “Dr. Jack” in the second questionnaire. Matching these requires a set of rules that can handle slight variations in the name field. These sets of rules are called fuzzy rules, and we call this process Fuzzy Name Matching.
Let’s formalize the problem. We have a database with ‘n’ tables that we want to join using the name attribute. Using a strict rule where we enforce that each character of a name in table1 should exactly match each character of a name in table2 is impractical, as is evident from the above example.
For example, the set of rules that we formulate should be able to match the name ‘Mike Daniel’ in Table 1 with ‘Mike D,’ ‘Dr. Mike’, ‘MikeDaniel’ etc.
Looking to extract information using Fuzzy Matching? Head over to Nanonets to use the solution that offers advanced Fuzzy Matching!
How to Perform Fuzzy Name Matching?
Many popular algorithms can be used to perform fuzzy name matching. The following section discusses some of those popular algorithms.
Fuzzy Name Matching Algorithms
1) Levenshtein Distance:
The Levenshtein distance is a metric that measures the difference between 2 string sequences.
It measures the number of single-character insertions, deletions, or substitutions required to change one string into another.
Mathematically, we can define the Levenshtein distance as follows :
Tail (a) is a string comprising all the characters in the string, excluding the first character. The definition clearly shows that the Levenshtein distance performs well with misspelled names.
For example, the Levenshtein distance (the number of single-character insertions, deletions, or substitutions) between the strings JOHN (as it is spelled in the US) and JOHAN (as it is spelled in Japan, Sweden, and Norway) ’ is 1 as shown in Fig7.
The most apparent drawback while using the Levenshtein distance is that it only considers the difference in how we spell words.
For example, The Levenshtein distance between the words “ROBERT” and “BOBBY” is 4. (NOTE: Bobby is a nickname for Robert)
2) The Soundex Algorithm:
Soundex is a phonetic algorithm that is used to search for names that sound similar but are spelled differently. It is most commonly used for genealogical database searches.
The Soundex algorithm outputs a 4-digit code given a name. (The Wikipedia page https://en.wikipedia.org/wiki/Soundex explains the Soundex algorithm well)For example, “Stuart” and “Stewart” produce the same Soundex code S363.
3) The Metaphone and Double Metaphone Algorithms:
The Metaphone algorithm is an improvement over the vanilla Soundex algorithm, while the double Metaphone algorithm builds upon the Metaphone algorithm. The ‘double’ Metaphone algorithm returns two keys for words with more than one pronunciation.
Let us consider the following example:Soundex (“Phillip”) = P410
Soundex (“Fillipe”) = F410
Doublemetaphone (“Phillip”) = FLP
Doublemetaphone (“Fillipe”) = FLP
We can see that the Doublemetaphone algorithm is much more robust than the Soundex algorithm.
Drawbacks:
A failure case I encountered was when I used the name Jesus (pronounced Haysoos in Spanish).
Doublemetaphone (‘Jesus’) = (‘JSS,’ ‘ASS’)
Doublemetaphone (‘Haysoos’) = (‘HSS,’ ‘ ’)
4) Cosine Similarity:
Cosine Similarity between two non-zero vectors equals the cosine of the angle between them.
If we represent each string (name) by a vector, we can compare the strings by measuring the angle between their corresponding vector representations.
If the vectors are parallel (theta=0 and cos(theta)=1), then they are equal to each other; however, if they are orthogonal(theta=90 degrees and cos(theta)=0), they are dissimilar.
Let us understand the various steps involved in computing the cosine similarity between two words with a simple example. Example: Name1 = “Johan”, Name2 = “John”.
i) Split the names into their corresponding “n-gram” representations.
ii) Vectorize each n-gram by using an encoding technique. The most commonly used encoding techniques are Bag-of-words encoding or , encoding.
iii) Compute the cosine similarity between the vectors.
Fig 8 illustrates all the steps in computing the vectors' cosine similarity.
Note: I was pretty surprised when I typed “Machine learning resources for fuzzy matching.” For once, I wasn’t flooded by hundreds of papers and their corresponding GitHub repositories.
Those interested can refer to the following link: https://www.cs.utexas.edu/~ml/papers/marlin-dissertation-06.pdf and the corresponding GitHub repository. It explains learnable similarity measures that can be trained for accurate record linkage, clustering, and blocking.
Looking to extract information using Fuzzy Matching? Head over to Nanonets to use the solution that offers advanced Fuzzy Matching!
What is the best Fuzzy Matching algorithm?
The best fuzzy matching algorithm depends on the case-to-case situation. The dataset requirements, the number of records combined with memory, and speed requirements help to determine the better algorithm.
Key Considerations for Fuzzy Matching
This section provides a few pointers as to how you can use fuzzy string matching to improve the existing workflow in your product or solution.
Assume your sales team needs help rolling out personalized content and products for potential customers due to mismanaged data storage.
Your best bet is to create a unified customer view that would aid your sales team in meeting their objectives. You decide to implement one or a combination of fuzzy string-matching algorithms to do the job. Here are a few points that you should keep in mind.
i) Time and resources required: It makes sense to invest a decent amount of time and resources in setting up the fuzzy string-matching software to suit your specific use case.
Rigorous unit testing is beneficial, especially if your use case demands high accuracy. The good news is that most of the workflow can be automated once you complete the software setup.
Considering the example of generating a unified customer view, the fuzzy matching software must be run regularly to ensure your view is updated.
ii) Reliability: How reliable would it be if you had spent time setting up the software? Almost every fuzzy string-matching algorithm is bound to generate some false positives.
This usually means some manual error checking. You have to find the right balance between the number of false positives, the amount of workforce you can afford for error checking, and the effect that the false positives would have on your company.
For example, if false positives result in a customer getting an advertisement for a pasta recipe instead of a pizza recipe, you are safe.
Best Practices for Fuzzy Matching
a) Fuzzy string matching is widely researched, and new algorithms/software are periodically released. It pays to keep your eyes and ears open for new developments.
b) Even after rigorous testing, you are bound to have a few false positives. Don't use fuzzy software to process sensitive data.
c) Fuzzy string matching pays the highest dividends when you have a lot of data that, if matched correctly, results in a significant upside, while false positives don't matter that much.
Looking to extract information using Fuzzy Matching? Head over to Nanonets to use the solution that offers advanced Fuzzy Matching!
Implementing Fuzzy Matching in Different Programming Languages
Let’s look at how Fuzzy Matching algorithms can be implemented in various programming languages.
We will implement fuzzy string matching in various programming languages on the restaurant dataset.
The dataset contains 864 restaurant records from Fodor’s and Zagat’s restaurant guides, including 112 duplicates (Source: https://www.cs.utexas.edu/users/ml/riddle/data.html) .
We illustrate an important application of fuzzy string matching, namely duplicate detection. For example, Consider Fig 10.
We can clearly see that the first and second records correspond to the same restaurant, and similarly, the third and fourth records correspond to the same restaurant. Our aim is to find all the duplicates in the database using fuzzy string matching.
In the process of implementing duplicate detection using various programming languages, we run through some of the in-built packages that these programming languages provide, using which almost all of the complexity is abstracted from the programmer.
To simplify the problem, we will attempt to detect duplicates only using the name field.
Fuzzy String Matching Using Python
Introducing Fuzzywuzzy: Fuzzywuzzy is a Python library for fuzzy string matching. Its basic comparison metric is the Levenshtein distance.
Using this basic metric, Fuzzywuzzy provides various APIs that can be directly used for fuzzy matching. Let us go through the entire pipeline of duplicate detection.
i) Data preprocessing:
Since we are detecting duplicates using only the ‘name’ field, in the preprocessing(data cleaning) stage we convert the entire name to lowercase and remove punctuation from the names. The code snippet in below illustrates this process.
ii) Creating an Index:
A naive way to match records in a table is to compare each record with every other record. However, using this method increases the number of pairs quadratically, which could slow down the algorithm.
We make use of the Python Record Linkage Toolkit, using which several indexing methods, such as blocking and sorted neighborhood indexing, can be implemented. (NOTE: For our dataset, we have computed a full index since it contains only 863 records)
The code snippet in below illustrates the creation of an index for record comparison.
iii) Identifying duplicates using Fuzzywuzzy:
Duplicates were identified using Fuzzywuzzy’s partial_ratio method. Given two strings, str1(length n1) and str2(length n2), such that n1 > n2, it computes the Levenshtein distance between str2 and all substrings of length n2 in str1.
Using this method, we identified 201 duplicates.
PolyFuzz is another library that uses multiple string similarity algorithms and can be customized for more specific matching tasks.
Fuzzy String Matching Using R
First, I must confess that I am an R virgin. However, it turns out that programming in R is extremely easy and intuitive. I performed the same steps namely data preprocessing (converting the names to lowercase and removing punctuation) followed by fuzzy name matching using the Levenshtein distance metric.
The following code snippet illustrates the pipeline used for duplicate detection.
Punctuation was eliminated by making use of the gsub function. Following this, a matrix was constructed using the Standard Levenshtein distance metric between the name fields.
Finally, the number of duplicates was counted (If the Levenshtein distance between any two records is lesser than 2, they are considered duplicates).
The algorithm detects 164 duplicate records.
Note: The above implementation isn't optimized.
Fuzzy String Matching Using Java
Things were a little tougher in Java, as it isn't specifically designed for data science. However, there are many GitHub repositories available that perform fuzzy string matching using Java.
The following repository https://github.com/xdrop/fuzzywuzzy contains a java implementation of the Fuzzywuzzy python library. A simple example is shown in below.
NOTE: The function tokenSortRatio splits the strings into tokens, sorts the individual tokens, and computes the Levenshtein distance between them.
The java string similarity package(https://github.com/tdebatty/java-string-similarity) implements a number of algorithms(Levenshtein edit distance, Jaro-Winkler, LCS etc).
Fuzzy Matching Without Using Any Code

Fear not; Microsoft Excel and tools like Nanonets can help you perform fuzzy string matching using the GUI interface.
Looking to extract information using Fuzzy Matching? Head over to Nanonets to use the solution that offers advanced Fuzzy Matching!
Fuzzy String Matching Using Microsoft Excel
Excel users might be familiar with the VLOOKUP function, which is used to find exact matches across columns in a table. On the desktop version, Excel also provides a Fuzzy Lookup add-in, which is used to perform fuzzy matching between columns.
At the time of writing this blog post, I was using a Linux-based operating system, so I wasn’t able to use the Fuzzy Lookup Add-in.
However, the web version of Microsoft Excel provides a similar add-in known as Exis Echo. It has an extremely simple interface; just select the desired number of rows from the columns that you want to match, and Exis Echo does the rest.
As shown above, the restaurants " hotel Bel-Air” and “Bel-Air Hotel” are identified as duplicates(i.e., they are placed in the same group). However, the algorithm doesn’t identify “art’s delicatessen” and “art’s deli” as the same restaurant.
The add-in provides several parameters that we can adjust for our specific use case.
Quick Comparison of Fuzzy Matching Software
The following is a comparison of the different languages or software that I used to implement fuzzy matching.
I have given a score out of 5, with 5 being the best and 1 being the worst.
| Software/Language Used | Ease of Use | Scalability | Speed | Total Overall Score |
|---|---|---|---|---|
| Python | 4.0 | 4.0 | 3.0 | 11.0 |
| R | 4.0 | 4.0 | 2.5 | 10.5 |
| Java | 2.0 | 3.0 | 5.0 | 10.0 |
| Microsoft Excel | 5.0 | 1.5 | 3.0 | 9.5 |
Scaling up Fuzzy Matching Implementation
So far, we have examined processing a few hundred records using fuzzy string matching. However, in the real world, we would deal with thousands, if not hundreds of thousands, of records.
In this section, we will introduce a few techniques that would help scale our fuzzy string-matching algorithm.
To illustrate this, I used a dataset containing a large number of company names. Let's run through the code, examine the function of each code snippet, and look at the corresponding output.
The above cell loads the data into a pandas dataframe. The dataset contains 1,040,569 entries.
Some data preprocessing is carried out in Cell2. The company names are converted into lowercase and all punctuation is removed from them.
We also define a list of common stop words such as “assn”, “inc” etc which we remove from the list of company names.
In Cell 3, we split the company names into n-grams, followed by vectorizing the company names using the Tf-idf function. The next step involves computing the cosine similarity between each pair of vectors in the tf_idf_matrix.
Doing this efficiently is crucial in ensuring that the approach scales well.
Scikit-learn provides an in-built function to compute the cosine similarity between vectors. However, the ING Wholesale Banking Advanced Analytics team has created a custom library called sparse_dot_topn to compute cosine similarity using Cython (https://github.com/ing-bank/sparse_dot_topn).
Their implementation improves speed by around 40%. I borrowed the code in cells4 and 5 from the following website: https://bergvca.github.io/2017/10/14/super-fast-string-matching.html.
The ‘matches’ matrix contains the indices and similarity scores used to identify duplicates. Since this dataset wasn’t specifically designed for duplicate detection or false positive identification, it was already cleaned up and didn’t contain any duplicates.
Note: I have uploaded the code to my Github repository. https://github.com/Varghese-Kuruvilla/Fuzzy_String_Matching.
I encourage you to use it as a reference for analyzing new datasets and understanding the basics of fuzzy string matching.
Looking to extract information using Fuzzy Matching? Head over to Nanonets to use the solution that offers advanced Fuzzy Matching!
Common Issues/Problems Faced with Fuzzy Matching and the Solution
In this section, I will try to answer some questions that I saw on StackOverflow while researching this blog post. I would encourage readers to read the entire post to get a good overall understanding of fuzzy string matching.
1) How to calculate the score in fuzzy string matching?
One of the most effective ways to calculate scores for a fuzzy string-matching algorithm is by using cosine similarity. The cosine similarity between two non-zero vectors is simply the cosine of the angle between these vectors.
Thus, two similar strings would have a higher cosine similarity score when compared to two dissimilar strings. The success of this method hinges on the manner in which strings are converted into their corresponding vector representations.
Two of the most popular methods for doing the same are The Bag-of-words(BOW) and TF-IDF feature extractors.
A BOW feature extractor computes the vector representation of a string by taking into account the frequency of each word in the document. A major shortcoming of the BOW feature extractor is that words like “the”, “of” etc are given a very high score since they appear very frequently in the document.
TF-IDF tries to overcome this problem by using information about the number of times the word appears in the document.
An example showing each of the individual steps in computing the cosine similarity is shown here

2) Fuzzy logic matching (https://stackoverflow.com/questions/37978098/fuzzy-logic-matching)
For your use case of matching lists of company names, I would suggest going through the following points.
a) Unique attribute: Firstly, make sure that you can’t match using any other unique attribute like an address, etc. A unique attribute would greatly simplify the problem. Having ensured that you only have the company name attribute for matching, you can proceed with the following steps.
b) Data preprocessing: Remove commonly occurring stop words from the text. Some manual processing, such as selecting the words that are not relevant to the list of company names from the most frequently occurring words, would prove useful.
c) Indexing: Comparing all the records is computationally expensive. An indexing method such as blocking or sorted neighborhood indexing can reduce the number of comparisons that have to be made.
d) Fuzzy Matching: A measure such as the Levenshtein distance can be used to calculate the scores between pairs of strings. The popular Python package Fuzzywuzzy covers several implementations of the Levenshtein distance.
For this use case, I would recommend using the token_set_ratio or the partial_ratio functions.
3) Fuzzy Search Algorithm(https://stackoverflow.com/questions/32337135/fuzzy-search-algorithm-approximate-string-matching-algorithm):
The problem can be broken down into two parts:
- Choosing the correct string metric.
- Coming up with a fast implementation of the same.
Choosing the correct metric: The first part is largely dependent on your use case. However, I suggest using a combination of a distance-based score and a phonetic-based encoding for greater accuracy, i.e., initially computing a score based on the Levenshtein distance and later using Metaphone or Double Metaphone to complement the results.
Again, you should base your decision on your use case, if you can do with using just the Metaphone or Double Metaphone algorithms, then you needn't worry much about the computational cost.
Implementation: One way to cap down the computational cost is to cluster your data into several small groups based on your algorithm and load them into a dictionary.
For example, If you can assume that your user enters the first letter of the name correctly, you can store the names based on this invariant in a dictionary.
So, if the user enters the name "National School" you need to compute the metric only for school names starting with the letter "N".
Conclusion
I hope that you had a good time reading about fuzzy logic.
We initially discussed fuzzy logic, its practical applications and use cases, things to consider if you choose to use fuzzy matching, the various algorithms used to implement fuzzy string matching, and their implementation in popular programming languages.
We humans are often unsure about our decisions; by our very nature, we are fuzzy. As long as we stay fuzzy, it only makes sense that the tools that we design should also be fuzzy. On that rather philosophical note, I will see you in the next blog post.



